مهم ترین فرمول‌های ریاضی

به گزارش گروه وب گردی خبرگزاری صدا و سیما؛ همانطور که می‌دانیم اشکال هندسی مختلفی در محیط پیرامون ما و ریاضیات وجود دارند که هر یک دارای مساحت، محیط و حجمی متفاوت می‌باشند و برای به دست آوردن محیط، حجم و مساحت اشکال مختلف فرمول‌های ریاضی مختلفی وجود دارند.

فرمول‌های ریاضی اشکال مختلف
در محیط پیرامون ما اشکال هندسی مختلفی وجود دارند که هر یک از این شکل‌ها دارای محیط، مساحت و حجمی متفاوت می‌باشند. محیط، مساحت و حجم اشکال با توجه به نوع آن‌ها به روش‌ها و فرومول‌هایی متفاوت به دست می‌آیند. 

حجم اشکال هندسی
حجم یک جسم در واقع به میزان فضایی گفته می‌شود که آن جسم اشغال می‌کند. یکای حجم در سیستم متریک متر مربع است، در حالت کلی حجم را به شکل فضایی در نظر می‌گیرند که بتوانند در آن هوا، آب یا جرم خاصی را قرار دهند.
محیط اشکال هندسی
محیط یا همان پیرامون در زبان هندسه به خط و مسیری می‌گویند که سطحی را در میان خود بگیرد. محیط در واقع به معنی فراگیرنده بوده و به بخش بیرونی از یک شکل گفته می‌شود. همان فاصله‌ای که روی لبه بیرونی یک شکل پیموده می‌شود تا به نقطه اولیه خود برگردیم، محیط است، خود این لبه بیرونی را نیز به اصطلاح محیط می‌گویند. می‌توانیم محیط هر شکلی را با قرار دهی یک نخ یا طناب بر روی دور تا دور لبه بیرونی آن اندازه گیری کنیم. به دست آوردن محیط اشکال مختلف کاربرد‌های علمی زیادی دارد، به عنوان نمونه فبل از خزید یک زمین باید محیط آن اندازه گیری شود. بعلاوه می‌توانیم ریسمان مورد نیاز برای پیچاندن به دور یک ماسوره را با اندازه گیری محیط ماسوره تعیین نماییم.

مساحت اشکال هندسی
مساحت یا پهنه بزرگی یک سطح دو بعدی را تعیین می‌نماید. تمامی سطح یا کف یک شکل هندسی مساحت آن شکل در نظر گرفته می‌شود، سطح می‌تواند مربوط به شکلی دو بعدی یا شکلی سه بعدی باشد. مساحت دارای پایه سیستم SI متر مربع m۲ می‌باشد که برابر با مساحت مربهی به ضلع یک متر است. قبل از این در ایران از یکا‌های بومی مثل گریب برای اندازه گیری مساحت استفاده می‌شده است. همچنین از دیگر واحد‌های اندازه گیری مساحت هکتار و کیلومتر مربع است که برای واحد‌های بزرگتر از آن‌ها استفاده می‌شود. در کشور انگلیس از واحد ایکر برای اندازه گیری سطح استفاده می‌گردد.

در ادامه این مطلب شما را با فرمول‌های ریاضی حجم، مساحت و محیط برخی از اشکال مهم هندسی آشنا می‌کنیم، همراه ما باشید.

فرمول‌های مربع
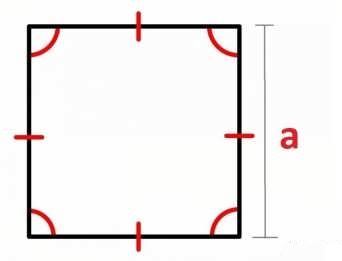
مربع یک چهار ضلعی منتظم می‌باشد که در آن تمامی اضلاع با هم برابر هستند و ضلع‌ها با هم دو به دو زاویه ۹۰ درجه را تشکیل می‌دهند.

مساحت مربع = یک ضلع × خودش
محیط مربع = یک ضلع × ۴

فرمول‌های مستطیل
مستطیل چهار ضلعی است که در آن تمامی زاویه‌ها قائمه هستند، مستطیل نوعی متوازی الاضلاع می‌باشد که در آن هر دو ضلع مجاور بر هم دیگر عمود باشند. یک مستطیل دارای خواص زیر است:

در مستطیل تمامی زوایا برابرند، مجموع زاویه‌های داخلی مستطیل برابر با ۳۶۰ درجه می‌باشد، قطر‌ها در مستطیل با هم برابرند، مستطیل‌ها دایره محیطی دارند، مستطیل دارای دو محور تقارن است، قطر‌ها در مستطیل محور تقارن نیستند.

مساحت یک مستطیل = طول × عرض
محیط یک مستطیل = ۲ × (طول + عرض)

فرمول‌های مثلت
مثلث که با نام‌های سه گوش و سه کنج نیز شناخته می‌شود یک چند ضلعی است که دارای سه ضلع باشد. مثلث همچنین شکلی مسطح می‌باشد که از اتصال سه نقطه غیر هم خط در صفحه ایجاد می‌شود. مثلث سه ضلع، سه زاویه و سه راس دارد، به شکلی دیگر مثلث از برخورد سه خط راست با یکدیگر به شکلی که هر سه قطع هم دیگر را قطع کنند به وجود می‌آید. مثلث سه گوش یا همان زاویه دارد که در آن مجموعه زاویه‌های داخلی برابر با ۱۸۰ درجه می‌باشد.

مساحت مثلث = ۲/ (قاعده × ارتفاع)
محیط مثلث = مجموعه سه ضلع مثلث

فرمول‌های مثلث متساوی الاضلاع
مثلث متساوی الاضلاع نوعی مثلث است که در آن ضلع‌ها با هم برابر باشند. اندازه هر زاویه داخلی در این مثلث برابر با ۶۰ درجه می‌باشد.

مساحت مثلث متساوی الاضلاع = ۲ / (ارتفاع × قاعده)
محیط مثلث متساوی الاضلاع = ۳ × یک ضلع

فرمول‌های مثلث متساوی الساقین
در مثلث متساوی الساقین دو ضلع با هم برابر هستند. این مثلث دارای دو زاویه داخلی برابر می‌باشد.

مساحت مثلث متساوی الساقین = ۲ / (ارتفاع × قاعده)
محیط مثلث متساوی الساقین = مجموع سه ضلع

فرمول‌های مثلث قائم الزاویه
مثلث قائم الزاویه، مثلثس است که یک زاویه قائمه داشته باشد، یعنی یکی از اضلاع آن بر یک ضلع دیگر عمود باشد.

مساحت مثلث قائم الزاویه = ۲ / (ارتفاع × قاعده)

محیط مثلث قائم الزاویه = مجموعه سه ضلع مثلث

فرمول‌های مخروط
مخروط نوعی شکل هندسی سه بعدی است که از سطح مقطع مخروط تا راس باریک می‌گردد. در واقع مخروط شکلی جامد می‌باشد که به یک صفحه مقطع محدود می‌گردد و سطح جانبی آن نیز مکان هندسی خطوط راستی می‌باشد که نوک مخروط را به نقطه‌های پیرامون پایه وصل می‌کنند. مخروط یک نوع هرم می‌باشد که قاعده آن دایره می‌باشد.

حجم مخروط = ۱/۳ مساحت قاعده × ارتفاع مخروط
مساحت مخروط = مساحت جانبی مخروط + مساحت قاعده

فرمول‌های ذوزنقه
ذوزنقه یکی از اشکال هندسی می‌باشد که دو بعدی بوده و دارای چهار ضلع می‌باشد. در ذوزنقه دو ضلع با هم موازی می‌باشند.

مساحت ذوزنقه = نصف ارتفاع × (قاعده بزرگ + قاعده کوچک)
محیط ذوزنقه = مجموع چهار ضلع

فرمول‌های لوزی
لوزی یک چهار ضلعی متساوی الاضلاع می‌باشد. در واقع لوزی یک چهار ضلعی است که اضلاعش دو به دو با هم برابر بوده و زاویه‌ای رو به روی آن‌ها با هم برابر می‌باشند. همچنین در لوزی قطر‌ها بر هم عمود هستند و هم دیگر را نصف می‌کنند. در لوزی مجموعه دو زاویه مجاور با هم برابر با ۱۸۰ درجه می‌باشد. در واقع متوازی الاضلاعی که در آن قطر‌ها بر هم عمود باشند لوزی است. ارتفاع لوزی طول یک خط عمود بر هر کدام از دو ضلع مقابل می‌باشد.

مساحت لوزی = ۲/ (قطر بزرگ × قطر کوچک)
محیط یک لوزی = ۴ × یک ضلع

متوازی الاضلاع
متوازی الاضلاع چهار ضلعی می‌باشد که در آن ضلع‌های رو به رو با هم همراستا و موازی باشند. در متوازی الاضلاع اضلاع و زاویه‌های رو به رو با هم برابر هستند. همچنین زاویه‌های مجاور با هم مکمل می‌باشند. مستطیل، لوزی و موبع یک نوع متوازی الاضلاع می‌باشند. در متوازی الاضلاع قطر‌ها هم دیگر را نصف می‌نمایند. فرمول‌های ریاضی متوازی الاضلاع عبارتند از:

مساحت متوازی الاضلاع = ارتفاع × قاعده
محیط متوازی الاضلاع = ۲ × مجموع دو ضلع متوالی

فرمول‌های دایره
دایره نوعی منحنی مسطح و بسته می‌باشد که شامل نقاطی از صفحه می‌شود که فاصله این نقاط از یک نقطه ثابت در آن صفحه مقداری ثابت است. نقطه ثابت را مرکز دایره می‌گویند و به این مقادیر ثابت، اندازه شعاع دایره گفته می‌شود.

شعاع دایره: پاره خطی است که مرکز دایره را به یکی از نقاط روی دایره متصل می‌کند، شعاع را معمولا با نام r مشخص می‌نمایند.

قطر دایره: قطر دایره به حداکثر فاصله بین دو نقطه روی محیط دایره گفته می‌شود. اندازه قطر دو برابر شعاع می‌باشد. قطر دایره از مرکز آن عبور می‌کند و دایره را به کمان‌هایی مساوی تقسیم می‌نماید. به این کمان‌ها نیم دایره می‌گویند. قطر دایره را در اکثر موارد با نام R نمایش می‌دهند. در ادامه با فرمول‌های ریاضی دایره آشنا می‌شویم.

مساحت دایره = عدد پی (۳/۱۴) × شعاع × شعاع
محیط دایره = عدد پی (۳/۱۴) × قطر
محیط دایره = عدد پی (۳/۱۴) × شعاع × ۲

فرمول‌های کره
کره یکی از حجم‌های هندسی سه بعدی می‌باشد که کاملا گرد است. کره مجموعه‌ای از تمام نقاط می‌باشد که در فاصله r (شعاع) از یک نقطه مشخص هستند. کره کاملا متقارن می‌باشد و دارای یال یا راس نیست.

مساحت کره = شعاع به توان ۲ × عدد پی (۳/۱۴) × ۴
حجم کره = شعاع به توان ۳ × عدد پی (۳/۱۴) × ۴/۳ (چهار سوم)

فرمول‌های بیضی
بیضی مجموعه‌ای از نقطه ا است که تمام نقاط آن در یک صفحه قرار داشته که فاصله نقاط از دو نقطه ثابت به اندازه‌ای ثابت باشند.

مساحت بیضی = ۳/۱۴ × (نصف قطر بزرگ × نصف قطر کوچک)

چند ضلعی منتظم
چند ضلعی منتظم، چند ضلعی می‌باشد که در آن تمامی زاویه‌ها و اضلاع هم اندازه باشند. این نوع چند ضلعی به اشکال کوژ یا ستاره هستند. چند ضلعی‌های منتظم دارای یک محیط محاطی هستند که به همه اضلاع در نقطه وسط آن‌ها مماس باشد. هر چند ضلعی منتظم لزوما یک چند ضلعی مماسی نیز می‌باشد. فرمول‌های ریاضی چند ضلعی شامل موارد زیر می‌شوند.

محیط چند ضلعی = طول یک ضلع × تعداد اضلاع آن
مساحت چند ضلعی = ۲ / (طول چند ضلعی × ارتفاع چند ضلعی) × تعداد اضلاع

مکعب مستطیل
مکعب مستطیل شکلی هندسی است که سه بعدی می‌باشد. مکعب مستطیل دارای شش وجه مستطیل شکل می‌باشد. مکعب مستطیل دارای ۸ گوشه و ۱۲ لبه می‌باشد. در این شکل هندسی تمامی زاویه‌ها قائمه هستند و وجوه رو به رو با هم برابر می‌باشند. مکعب حالتی از مکعب مستطیل می‌باشد.

حجم مکعب مستطیل = ارتفاع × طول × عرض
مساحت مکعب مستطیل برابر است با مجموع مساحت وجه‌های آن

فرمول‌های مکعب
مکعب یک شکل بسته سه بعدی می‌باشد که از شش مربع تشکیل می‌شود، در مکعب هر ضلع مربع فقط با یک ضلع از مربع دیگر مشترک می‌باشد و در راس‌ها سه مربع با هم ارتباط دارند. می‌توان مکعب را یک شش وجهی منتظم نامید که یکی از پنج جسم افلاطونی می‌باشد. مکعب همان مکعب مربع است. فرمول‌های ریاضی مکعب عبارتند از:

حجم مکعب = مساحت قاعده × ارتفاع
مساحت مکعب = مساحت قاعده × ۶

فرمول‌های هرم
هرم یکی از اشکال سه بعدی می‌باشد، هرم دارای یک سطح مسطح به نام قاعده هرم می‌باشد. قاعده هرم چند ضلعی دلخواه می‌باشد که به مثلث‌های هم راس وصل شده است. خط قائمی که راس هرم را به قاعده آن وصل می‌کند ارتفاع هرم نامیده می‌گردد. هرم همانطور که گفتیم یک چند وجهی می‌باشد که اگر قاعده آن مثلث باشد به آن هرم مثلث القاعده و اگر قاعده آن مربع باشد به آن هرم مربع القاعده گفته می‌شود. همچنین اگر قاعده هرم دایره باشد به آن مخروط می‌گوییم.

حجم هرم = (ارتفاع هرم × مساحت قاعده‌ی هرم) ۱/۳
مساحت هرم = مساحت قاعده + مساحت جانبی

فرمول‌های استوانه
استوانه یکی از انواع اشکال هندسی منحنی فضایی در هندسه می‌باشد که سطح دور آن از نقاطی تشکیل می‌شود که در فاصله یکسانی از یک خط راست قرار داشته باشند. به این خط راست محور گفته می‌شود. دو سر استوانه به کمک دو صفحه عمود بر محور استوانه بسته می‌گردد.

مساحت جانبی استوانه = محیط قاعده × ارتفاع
حجم استوانه = مساحت قاعده × ارتفاع
سطح کل استوانه = مساحت دو قاعده + مساحت جانبی
مساحت جانبی استوانه = مساحت مجموع دو قاعده + (ارتفاع × محیط قاعده)

منشور
منشور به یک چند وجهی می‌گویند که دو قاعده n ضلعی دارد. قاعده‌ها در آن در دو صفحه موازی قرار گرفته اند و قاعده‌ها همنهشت می‌باشند. n وجه دیگر منشور لزوما همه متوازی الاضلاع هستند و راس‌های متناظر دو n-ضلعی را به هم وصل می‌نمایند. تمامی سطح مقطع‌های موازی با قاعده، یکسان می‌باشند. منشور‌ها با توجه به تعداد اضلاع قاعده خود نام گذاری می‌گردند. به همین خاطر یک منشور با قاعده سه ضلعی منشور سه پهلو نامیده شده است. در ادامه با فرمول‌های ریاضی منشور آشنا می‌شویم.

فرمول‌های ریاضی منشور عبارتند از:

مساحت جانبی منشور = مجموع مساحت‌های سطوح جانبی منشور
مساحت کل منشور = مجموع مساحت دو قاعده + مساحت جانبی منشور
حجم منشور= مساحت قاعده × طول منشور